calendarBack
Quant

/

Geometry

/

Circles
ALL MODULES

CAT 2025 Lesson : Circles - Chord Properties

bookmarked

5. Chord

A chord is a line segment that has both its end points on the circumference of a circle.

Properties Figure
Centre-Chord Relationships: 1) A line drawn from the centre of a circle to a chord's midpoint is perpendicular to the chord.
2) A perpendicular line drawn from the centre of the circle to a chord, bisects the chord.
3) Perpendicular bisector of a chord passes through the centre.

O is the centre of the circle. C is the midpoint of the chord AB.
Angle at centre: Equal chords subtend equal angles at the centre. The same hold goods for arcs as well.

AB and CD are equal chords. So, they subtend equal angles at the centre, i.e., ∠\angleAOB == ∠\angleCOD
Angle on Circle: Equal chords subtend equal angles on the circle along their respective major or minor arcs

Here, we consider the angles subtended by the equal chords in its minor axis. AB and CD are the equal chords, so ∠\angleAXB == ∠\angleCYD

The angles subtended by the equal chords are in their respective major axis (indicated with dotted lines). AB and CD are the equal chords, so ∠\angleAPB == ∠\angleCQD

Equidistant chords: 1) Equal chords are equidistant from the centre of the circle, i.e., the perpendiculars drawn from the centre of the circle to the equal chords are equal.

2) Chords equidistant from centre are equal, i.e., if the perpendiculars, drawn from the centre of the circle to respective chords, are equal, then the chords are equal.

Here, AB and CD are equal chords. OX and OY are perpendiculars drawn from O to the chords AB and CD. So, OX == OY
Internal Chords Intersection: When two chords intersect the product of the parts formed by one chord is equal to the product of parts formed by the other.

Chords AB and CD intersect at point P inside the circle, so PA ×\times PB == PC ×\times PD
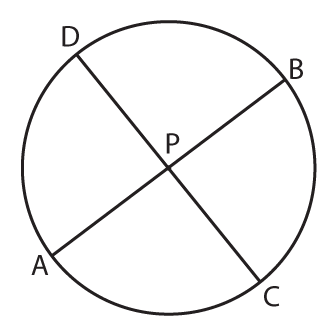External Chords intersection: If the same chords are positioned to intersect outside the circle, then the product of each chord and the chord along with its part outside the circle is equal to the respective product for the other chord.

Chords AB and CD intersect at point P outside the circle, so PA ×\times PB == PC ×\times PD

Example 4

In the figure below, O is the centre of the larger circle where XY is a chord of length 1010 cm and XY is also the diameter of the circle drawn through O, X and Y. P is the mid-point of XY and the line joining O and P intersects the larger circle at Q. What is the length of PQ in cm?

(1) 2\sqrt{2}           (2) 5−2\sqrt{5} - \sqrt{2}           (3) 5(2−1)5(\sqrt{2} - 1)           (4) 5(2+1)\sqrt{5}(\sqrt{2} + 1)          

Solution

As P is the mid-point of XY, which is the diameter of the smaller circle, P is the centre of the smaller circle. As XY == 1010 cm, PX == PY == PO == 55 cm

The line joining the mid-point of a chord with the centre of the circle is perpendicular to the chord.
∴\therefore △\triangleOPX is an isosceles right-angled triangle, where the angles are 45o−45o−90o45^\mathrm{o} - 45^\mathrm{o} - 90^\mathrm{o}, whose sides opposite to these angles will be in the ratio 1:1:21 : 1 : \sqrt{2}.

∴\therefore As PO =5= 5 cm, OX =52= 5\sqrt{2} cm

Radius of larger circle == OX == OQ == 525\sqrt{2} cm

PQ == OQ −- OP == 52−5=5\sqrt{2} - 5 = 5(2−1)5(\sqrt{2} - 1)

Answer: 5(2−1)5(\sqrt{2} - 1)


Example 5

A circle with 1717 cm radius is drawn with O as the centre. In this circle, chords AB and CD intersect at E such that EC =6= 6 cm and CD =26= 26 cm. If AB passes through O, then what is the length of BE (in cm) if O lies between A and E?

Solution

ED == CD −- EC = 26−6=2026 - 6 = 20 cm

As the radius is 1717 cm, the diameter AB has a length of 3434 cm.

Let BE = xx. Then, AE = 34−x34 - x

x(34−x)=6×20x(34 - x) = 6 \times 20
⇒ x2−34x+120=0x^{2} - 34x + 120 = 0
⇒ (x−4)(x−30)=0(x - 4) (x - 30) = 0

x=4x = 4 (x=30x = 30 is rejected as BE < AE)

Answer: 44


Want to read the full content

Unlock this content & enjoy all the features of the platform

Subscribe Now arrow-right
videovideo-lock