Plans
Dashboard
Daily & Speed
Quant
Verbal
DILR
Compete
Free Stuff
Circles
MODULES
Terminologies
Circumference & Area
Chord Properties
Angle Properties
Quadrilaterals in Circles
Tangents
Common Tangents
Past Questions
CONCEPTS & CHEATSHEET
Concept Revision Video
PRACTICE
Circles : Level 1
Circles : Level 2
Circles : Level 3
ALL MODULES
CAT 2025 Lesson : Circles - Common Tangents
9. Common Tangents
| Properties | Figure |
|---|---|
| When one circle is inside the other, then there can be no common tangent. |  |
| When two circles touch internally at exactly one point, then there can be a maximum of 1 common tangent. The two circles touch at A. The common tangent that can be drawn is a |
 |
| When two circles intersect each other at 2 points, then 2 common tangents can be drawn. |  |
| When two circles touch externally at exactly one point, then there can be a maximum of 3 common tangents. Here, the two circles touch at A. The common tangents that can be drawn are a,b and c |
 |
| When two non- overlapping circles do not touch each other, then there can be a maximum of 4 common tangents. The tangents that do not intersect each other are called direct tangents and the tangents that do not intersect each other are called transverse tangents. In the two circles, AB and CD are the direct common tangents EF and GH are the transverse common tangents Where r1 & r2 are the radii of the circles with O & P as centres, AB2 = CD2 = OP2−(r1−r2)2 EF2 = GH2 = OP2−(r1+r2)2 |
 |
10. Semicircle
Area of a semicircle = 2πr2 and Circumference of a semicircle = πrExample 15
What is the minimum possible ratio of the area of a semicircle to the area of the largest square that can be inscribed in the semicircle, such that one of the sides of the square lies on the diameter of the semicircle?
(1) 5π:4 (2) 5π:8 (3) 4π:5 (4) 8π:5
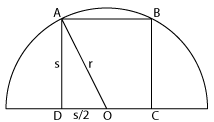
Let CD lie on the diameter, while A and B lie on the arc. Where r is the radius and s is the side of the square, OA = r and AD = s
△OAD ≅ △OBC (RHS congruency)
∴ OC = OD = 2s
Applying pythagoras theorem, r2=s2+(2s)2 = 45s2
Ratio of area of semicircle to square = 2πr2:s2 = π85s2:s2 = 5π:8
Answer: (2) 5π:8
(1) 5π:4 (2) 5π:8 (3) 4π:5 (4) 8π:5
Solution
| To minimise the ratio, the area of the square which is in the denominator should be maximised. If one of the sides is on the diameter of the circumcircle, the area of the square will be maximum when the other two vertices lie on the arc of the semicircle. |
 |
Let CD lie on the diameter, while A and B lie on the arc. Where r is the radius and s is the side of the square, OA = r and AD = s
△OAD ≅ △OBC (RHS congruency)
∴ OC = OD = 2s
Applying pythagoras theorem, r2=s2+(2s)2 = 45s2
Ratio of area of semicircle to square = 2πr2:s2 = π85s2:s2 = 5π:8
Answer: (2) 5π:8
Want to read the full content
Unlock this content & enjoy all the features of the platform
Subscribe Now