+91 9600 121 800

Plans

Dashboard

Daily & Speed

Quant

Verbal

DILR

Compete

Free Stuff

calendarBack
Quant

/

Geometry

/

Circles

Circles

MODULES

Terminologies
Circumference & Area
Chord Properties
Angle Properties
Quadrilaterals in Circles
Tangents
Common Tangents
Past Questions

CONCEPTS & CHEATSHEET

Concept Revision Video

PRACTICE

Circles : Level 1
Circles : Level 2
Circles : Level 3
ALL MODULES

CAT 2025 Lesson : Circles - Quadrilaterals in Circles

bookmarked

7. Inscribed & Circumscribed Quadrilaterals

Properties Figure
Concyclic Property: If a line segment subtends equal angles at its same side, then the end points of the line segment and the vertices of the equal angles are concyclic, i.e., all the points lie on the same circle.

AB subtends equal angles at C and D, i.e., ∠\angle∠ADB =∠= \angle=∠ACB.

∴\therefore∴ A, B, C and D are concyclic and lie on the same circle.
Cyclic Quadrilateral: A quadrilateral which can be circumscribed by a circle, i.e., where the 444 vertices are concyclic.

Property 1: The sum of any two opposite angles of a cyclic quadrilateral is 180o180^\mathrm{o}180o.

∠1+∠3=∠2+∠4=180o\angle1 + \angle3 = \angle2 + \angle4 = 180^\mathrm{o}∠1+∠3=∠2+∠4=180o

Property 2: An exterior angle of a quadrilateral is equal to its interior opposite angle.

∠5=\angle{5} =∠5= ∠3\angle{3}∠3, ∠6=\angle{6} =∠6= ∠4\angle{4}∠4
∠7=\angle{7} =∠7= ∠1\angle{1}∠1, ∠8=\angle{8} =∠8= ∠2\angle{2}∠2

Property 3: The product of the length of diagonals is equal to the sum of the product of the lengths of the opposite sides (Ptolemy's Theorem).

AC ×\times× BD = AB ×\times× CD +++ BC ×\times× DA

Property 4: Where a,b,ca, b, ca,b,c and ddd are the lengths of the sides of the cyclic quadrilateral and s=s =s= a+b+c+d2\dfrac{a + b + c + d}{2}2a+b+c+d​

Area =(s−a)(s−b)(s−c)(s−d)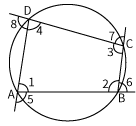= \sqrt{(s - a)(s - b)(s - c)(s - d)}=(s−a)(s−b)(s−c)(s−d)​



Tangential Quadrilateral: The sum of opposite sides of a tangential quadrilateral are equal.

Here, AB +++ CD === BC +++ DA

Example 8

In the diagram below, A, B, C and D lie on a circle. ∠\angle∠ABC === 70o70^\mathrm{o}70o and ∠\angle∠BCD === 130o130^\mathrm{o}130o. BA and CD are extended to points F and E respectively such that ∠\angle∠FAE === ∠\angle∠BAD. What is the value of ∠\angle∠DEA?

Solution

As ABCD is a cyclic quadrilateral,
∠\angle∠ABC =∠= \angle=∠ADE =70o= 70^\mathrm{o}=70o (Exterior ∠\angle∠ === Interior Opposite ∠\angle∠)

∠\angle∠BAD === 180o180^\mathrm{o}180o −-− ∠\angle∠BCD === 50o50^\mathrm{o}50o (Sum of Opposite ∠\angle∠ === 180o180^\mathrm{o}180o)

The question states ∠\angle∠FAE === ∠\angle∠BAD === 50o50^\mathrm{o}50o ∠\angle∠FAE + ∠\angle∠DAE +++ ∠\angle∠BAD === 180o180^\mathrm{o}180o (∠\angle∠ es on a straight line)
⇒ ∠\angle∠DAE === 180o−50o−50o180^\mathrm{o} - 50^\mathrm{o} - 50^\mathrm{o}180o−50o−50o === 80o80^\mathrm{o}80o

∠\angle∠AED +++ ∠\angle∠DAE +++ ∠\angle∠ADE === 180o180^\mathrm{o}180o (Sum of ∠\angle∠ es of triangle)
⇒ ∠\angle∠AED +++ 80o+70o=180o80^\mathrm{o} + 70^\mathrm{o} = 180^\mathrm{o}80o+70o=180o
⇒ ∠\angle∠AED === 30o30^\mathrm{o}30o

Answer: 30o30^\mathrm{o}30o


Example 9

In quadrilateral ABCD, AB, BC, CD and DA are the tangents of a circle with centre O. If AB === 555 cm and BC === 777 cm, then what is the difference in the lengths (in cm) of CD and DA?

Solution

As ABCD is a tangential quadrilateral, the sum of its opposite sides are equal.

∴\therefore∴ AB +++ CD === BC +++ DA
⇒ 555 +++ CD === 777 +++ DA
⇒ DA −-− CD === 222

∴\therefore∴ Difference between DA and CD is 222 cm.

Answer: 222


Want to read the full content

Unlock this content & enjoy all the features of the platform

Subscribe Now arrow-right
videovideo-lock