+91 9600 121 800

Plans

Dashboard

Daily & Speed

Quant

Verbal

DILR

Compete

Free Stuff

calendarBack
Quant

/

Geometry

/

Circles

Circles

MODULES

Terminologies
Circumference & Area
Chord Properties
Angle Properties
Quadrilaterals in Circles
Tangents
Common Tangents
Past Questions

CONCEPTS & CHEATSHEET

Concept Revision Video

PRACTICE

Circles : Level 1
Circles : Level 2
Circles : Level 3
ALL MODULES

CAT 2025 Lesson : Circles - Tangents

bookmarked

8. Tangents

Properties Figure
Property 1:From any external point, exactly two tangents can be drawn to meet a circle. The length of the these two tangents are equal.

Here, from external point P, PA and PB are the only tangents that can be drawn and PA === PB
Property 2:From any point on a circle, only one tangent can be drawn.

Here, through the points A, B and C that lie on the circle the only tangents that can be drawn are x,yx, yx,y and zzz respectively.
Property 3:The line connecting the centre of the circle to the point where a tangent meets the circle is perpendicular to the tangent.

ttt is the tangent passing through B. Therefore, OB is perpendicular to ttt.
Property 4:If two tangents are drawn to a circle from an external point, then the line joining the the centre of the circle and this external point,
1) bisects the angle subtended by the tangents at the external point
2) bisects the central angle formed by the points where the common tangents touch the circle
3) is perpendicular to the line formed by joining the points where the common tangents touch the circle

PA and PB are the two common tangents that touch the circle at A and B respectively. O is the centre of the circle. So,
1) ∠\angle∠APO === ∠\angle∠BPO
2) ∠\angle∠AOP === ∠\angle∠BOP
3) AB is perpendicular to PO
Tangent-Secant Theorem:If a tangent and a secant are drawn to a circle from an external point, then the square of the length of the tangent equals the product of distances of the external point to the two intersection points of the circle.

Here, PT is the tangent of the circle and PB is the secant intersecting the circle at A and B. So, PT2^{2}2 === PA ×\times× PB.
Alternate Segment Theorem : The angle subtended by a chord and a tangent on one side equals the angle subtended by the chord in the alternate segment.

Here, XY is the tangent intersecting the circle at B. BC and BD are two chords. So, ∠\angle∠DBX === ∠\angle∠BCD and ∠\angle∠CBY === ∠\angle∠BDC.

Example 10 to 12

In the adjoining diagram, I and II are circles with centres P and Q respectively. The two circles touch each other and have a common tangent that touches them at points R and S respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the ratio 4:34 : 34:3. It is also known that the length of PO is 282828 cm
[CAT 2004]

10) What is the ratio of the length of PQ to that of QO?

(1) 1:41 : 41:4                     (2) 1:31 : 31:3                     (3) 3:83 : 83:8                      (4) 3:43 : 43:4                    

11) What is the radius of circle II?

(1) 222 cm                    (2) 333 cm                    (3) 444 cm                      (4) 5 cm                   

12) The length of SO is

(1) 838\sqrt{3}83​cm              (2) 10310\sqrt{3}103​cm              (3) 12312\sqrt{3}123​cm               (4) 14314\sqrt{3}143​cm             

Solution

PR and QS are the radii of circles I and II.
Also, PR and QS are perpendicular to the tangent OR.

As the ratio of diameters of the circles is 4:34 : 34:3, let the radii PR and QS be 4x4x4x and 3x3x3x respectively.

△\triangle△OSQ ~ △\triangle△ORP [As ∠\angle∠OSQ === ∠\angle∠ORP === 90o90^\mathrm{o}90o & ∠\angle∠O is common)

OQOP=QSPR\dfrac{OQ}{OP} = \dfrac{QS}{PR}OPOQ​=PRQS​ ⇒ OP−7xOP=3x4x\dfrac{OP - 7x}{OP} = \dfrac{3x}{4x}OPOP−7x​=4x3x​
As OP =28= 28=28,

⇒ 28−7x28=34\dfrac{28 -7x}{28} = \dfrac{3}{4}2828−7x​=43​ ⇒ x=1x = 1x=1

∴\therefore∴ PR =4= 4=4 cm, QS =3= 3=3 cm, PQ =7= 7=7 cm & QO === 28−7=2128 - 7 = 2128−7=21 cm

10) PQ : QO === 7:21=1:37 : 21 = \bm{1 : 3}7:21=1:3

11) Radius of circle II === QS === 3\bm{3}3 cm

12) △\triangle△OSQ is a right-angled triangle. Therefore, applying Pythagoras theorem,
OS2^{2}2 + QS2^{2}2 === OQ2^{2}2
⇒ OS2+32^{2} + 3^{2}2+32 === 21221^{2}212 ⇒ OS === 432=123\sqrt{432} = \bm{12\sqrt{3}}432​=123​ cm

Answer: 10) (2) 1:31 : 31:3 ; 11) (2) 333 cm ; 12) (3) 12312\sqrt{3}123​ cm


Example 13

From an external point P, the 222 tangents drawn to the circle with centre O meet the circle at points A and B such that ∠\angle∠APB === 30o30^\mathrm{o}30o. A third tangent drawn through a point on the minor arc AB intersects PA and PB at C and D respectively. What is ∠\angle∠COD?

Solution

The line from the centre to a point on the circle is perpendicular to the tangent that passes through the point.
∴\therefore∴ PA ⊥\perp⊥ OA, PB ⊥\perp⊥ OB & CD ⊥\perp⊥ OE

Sum of interior angles of quadrilateral OAPB === 360o360^\mathrm{o}360o

⇒ ∠\angle∠AOB + ∠\angle∠PAO + ∠\angle∠BPA + ∠\angle∠OBP === 360o360^\mathrm{o}360o
⇒ ∠\angle∠AOB + 90o+30o+90o=90^\mathrm{o} + 30^\mathrm{o} + 90^\mathrm{o} =90o+30o+90o= 360o360^\mathrm{o}360o
⇒ ∠\bm{\angle}∠AOB =150o\bm{= 150^\mathrm{o}}=150o

CE === CA, OE === OA and ∠\angle∠CEO === ∠\angle∠CAO === 90o90^\mathrm{o}90o
△\triangle△COE ≅ △\triangle△COA (SAS congruency)

∴\therefore∴ ∠\angle∠AOC === ∠\angle∠COE === 12×\dfrac{1}{2} \times21​× ∠\angle∠AOE

Likewise, △\triangle△DOE ≅ △\triangle△DOB (SAS congruency)

∴\therefore∴ ∠\angle∠BOD === ∠\angle∠DOE === 12×\dfrac{1}{2} \times21​× ∠\angle∠BOE

∠\angle∠COD === ∠\angle∠COE +++ ∠\angle∠DOE === 12×\dfrac{1}{2} \times21​× ∠\angle∠AOE +++ 12×\dfrac{1}{2} \times21​× ∠\angle∠BOE

=== 12×\dfrac{1}{2} \times21​× (∠\angle∠AOE +++ ∠\angle∠BOE ) === 12×\dfrac{1}{2} \times21​× ∠\angle∠AOB

=== 12×150=75o\dfrac{1}{2} \times 150 = \bm{75^\mathrm{o}}21​×150=75o

Answer: 75o75^\mathrm{o}75o


Example 14

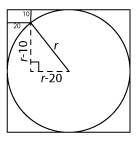
In the adjoining figure, the rectangle at the corner measures 101010 cm ×20\times 20×20 cm. The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?
[CAT 2003L]

(1) 101010 cm            (2) 404040 cm            (3) 505050 cm            (4) None of the above           

Solution

Let the radius of the circle be rrr cm.

When the vertical side is extended down and a line is drawn from the centre O that is parallel to the 202020 cm side, the two lines are perpendicular to each other.

We now get a right-angled triangle with r being the hypotenuse. The other 222 sides are (r−10)(r - 10)(r−10) cm and (r−20)(r - 20)(r−20) cm.

Substituting values, we note that r=50r = 50r=50 cm results in the other 222 sides being 404040 cm and 303030 cm.

As 302+402=50230^{2} + 40^{2} = 50^{2}302+402=502, r=50\bm{r = 50}r=50 cm is the answer.

Answer: (3) 505050 cm


Want to read the full content

Unlock this content & enjoy all the features of the platform

Subscribe Now arrow-right
videovideo-lock