+91 9600 121 800

Plans

Dashboard

Daily & Speed

Quant

Verbal

DILR

Compete

Free Stuff

calendarBack
Quant

/

Geometry

/

Lines & Triangles

Lines And Triangles

MODULES

Lines & Angles
Parallel Lines
Basics of Triangles
Types of Triangles
Triangle & its Segments
Area of a Triangle
Isosceles & Equilateral
Right-angled Triangles
Other Theorems
Congruency & Similarity
Past Questions

CONCEPTS & CHEATSHEET

Concept Revision Video

SPEED CONCEPTS

Lines & Triangles 1
-/10
Lines & Triangles 2
-/10
Lines & Triangles 3
-/10

PRACTICE

Lines & Triangles : Level 1
Lines & Triangles : Level 2
Lines & Triangles : Level 3
ALL MODULES

CAT 2025 Lesson : Lines & Triangles - Parallel Lines

bookmarked

2.1 Parallel Lines & Transversal

The concept and properties of parallel lines and transversal will be used across geometry. These properties are used to prove many geometrical theorems.

Parallel lines are two or more line that do not intersect each other. The distance between parallel lines remains the same throughout the plane they belong.
Two or more lines that make the same angle with respect to another common line are parallel to each other.


In the figure above, lines AB, CD and EF subtend the line l\bm{l}l at 30°30\degree30°, so they are parallel and the line l, which intersects the parallel lines, is called the transversal.

In a system with 222 or more parallel lines and transversals, an intercept is the distance, measured on the transversal, between 222 parallel lines. In the figure, BD, DF and BF are the intercepts.

In the below figure, AB | | CD | | EF and l & m are the transversals. PQ & QR are the intercepts on lll and XY & YZ are the intercepts on mmm.

According to Basic Proportionality Theorem, PQ : QR = XY : YZ



In the following figure, we observe the types of angles formed in a system with parallel lines and transversals.



When parallel lines AB & CD are intersected by a transversal l\bm{l}l

Corresponding angles are equal ∠1=∠5,∠2=∠6\angle{1} = \angle{5}, \angle{2} = \angle{6}∠1=∠5,∠2=∠6
∠3=∠7,∠4=∠8\angle{3} = \angle{7}, \angle{4} = \angle{8}∠3=∠7,∠4=∠8
Alternate Interior angles are equal. ∠3=∠6,∠4=∠5\angle{3} = \angle{6}, \angle{4} = \angle{5}∠3=∠6,∠4=∠5
Alternate Exterior angles are equal. ∠3=∠8,∠2=∠7\angle{3} = \angle{8}, \angle{2} = \angle{7}∠3=∠8,∠2=∠7
Interior angles on the same side of the transversal are supplementary. ∠3+∠5=180°\angle{3} + \angle{5} = 180\degree∠3+∠5=180°
∠4+∠6=180°\angle{4} + \angle{6} = 180\degree∠4+∠6=180°
Exterior angles on the same side of the transversal are supplementary. ∠1+∠7=180°\angle{1} + \angle{7} = 180\degree∠1+∠7=180°
∠2+∠8=180°\angle{2} + \angle{8} = 180\degree∠2+∠8=180°
Vertically Opposite Angles (formed when two lines intersect) are equal. ∠1=∠4\angle{1} = \angle{4}∠1=∠4, ∠2=∠3\angle{2} = \angle{3}∠2=∠3
∠5=∠8\angle{5} = \angle{8}∠5=∠8, ∠6=∠7\angle{6} = \angle{7}∠6=∠7


Example 4

In the following figure, AB, CD and EF are parallel lines. What is the length of BF?


Solution

Let BF = xxx cm

2050=12x\dfrac{20}{50} = \dfrac{12}{x}5020​=x12​ ⇒ x=30x = 30x=30

Answer: 303030 cm

Example 5

In the following figure, PQ | | RS. Then, ∠\angle∠C = ?

Solution

If we draw a parallel line TU which passes through C, then
∠\angle∠QAC = ∠\angle∠ACT = 35°35\degree35° (Alternate interior angles are equal)
∠\angle∠SBC = ∠\angle∠BCT = 25°25\degree25° (Alternate interior angles are equal)

∴\therefore∴ ∠\angle∠ACB = 35°+25°35\degree + 25\degree35°+25° = 60°60\degree60°


Alternatively
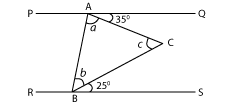If we join AB, this becomes the transveral.
QAB + SBA = 180°180\degree180° (Interior angles )
a+ba + ba+b = 180°−25°−35°=120°180\degree - 25\degree - 35\degree = 120\degree180°−25°−35°=120°

a+b+c=180°a + b + c = 180\degreea+b+c=180° (Sum of angles of a triangle)
⇒ c=180°−120°=60°c = 180\degree - 120\degree = 60\degreec=180°−120°=60°


Answer: 60°60\degree60°


Want to read the full content

Unlock this content & enjoy all the features of the platform

Subscribe Now arrow-right
videovideo-lock