CAT 2025 Lesson : Set Theory - Set Operations & Venn Diagram

3. Set Operations & Venn Diagram

In Venn diagrams, we use circles or other closed objects to represent sets. Intersections are the regions that represent the common elements of the sets. An enclosing rectangle drawn represents the universal set.

Union of sets: Union of two sets A and B is the set containing all elements of set A or set B or both. This is denoted as A $\cup$ B.
Intersection of sets: Intersection of two sets A and B is the set containing all elements that are in both set A and set B. This is denoted as A $\cap$ B.
Difference in sets: Difference of sets A and is the set containing all elements of set A that are not in set B. This is denoted as A - B.
Complement of Sets: If A is set that is a subset of a universal set U (A $\subseteq$ U), then the complement of A is a set containing all elements in U that are not in A. A' or $\text{A}^{c}$ is used to denote the complement of a set A.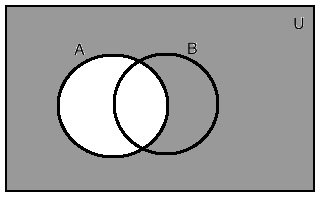
Disjoint Sets: Disjoint sets are sets which do not have any element common between them. A $\cap$ B $= \phi$ .

3.1 Laws in Sets

Type	Laws
Identity Law	A $\cup \ \phi =$ A A $\cap$ $=$ A
Commutative Law	A $\cup$ B $=$ B $\cup$ A A $\cap$ B $=$ B $\cap$ A
Associative Law	A $\cup$ (B $\cup$ C) $=$ (A $\cup$ B) $\cup$ C A $\cap$ (B $\cap$ C) $=$ (A $\cap$ B) $\cap$ C
Distributive Law	A $\cup$ (B $\cap$ C) $=$ (A $\cup$ B) $\cap$ (A $\cup$ C) A $\cap$ (B $\cup$ C) $=$ (A $\cap$ B) $\cup$ (A $\cap$ C)
De-Morgan's Law	(A $\cup$ B)' $=$ A' $\cap$ B' (A $\cap$ B)' $=$ A' $\cup$ B'

Note: The above laws are easy to observe in Venn diagrams. As these are generally not tested in entrance tests, you can choose not to memorise these.

3.2 Cardinal number of sets and associated formulae

n(\text{A} \cup \text{B})

= n(\text{A}) + n(\text{B}) - n(\text{A} \cap \text{B})

2) Where the sets are disjoint,

A \cap B

= \phi

. So, in disjoint sets,

n (\text{A} \cup \text{B})

= n(\text{A}) + n(\text{B})

n(\text{A} \cup \text{B} \cup \text{C})

= n(\text{A}) + n(\text{B}) + n(\text{c}) - n(\text{A} \cap \text{B}) - n(\text{B} \cap \text{C}) - n(\text{A} \cap \text{C})

+ n(\text{A} \cap \text{B} \cap \text{C})

Want to read the full content

Unlock this content & enjoy all the features of the platform

Subscribe Now